Pensez en Python

Nous allons définir une classe appelée Temps, qui enregistre le moment de la journée et constituera un nouvel exemple de type défini par le programmeur. La définition de la classe ressemble à ceci :

class Temps:
    """Représente le moment de la journée.
       
    attributs : heure, minute, seconde
    """

Nous pouvons créer un nouvel objet de type Temps et attribuer des valeurs à heures, minutes et secondes :

moment = Temps()
moment.heure = 11
moment.minute = 59
moment.seconde = 30

Le diagramme d'état pour l'objet Temps ressemble à la figure 16.1.

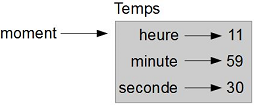
À titre d'exercice, écrivez une fonction appelée afficher_temps qui prend un objet Temps et l'affiche dans la forme heure:minute:seconde. Indice : la séquence de formatage '%.2d' affiche un entier en utilisant au moins deux chiffres, en ajoutant un zéro en début si nécessaire.

Écrivez une fonction booléenne nommée est_apres qui prend deux objets Temps, t1 et t2, et retourne True si t1 suit chronologiquement t2 et False sinon. Défi : n'utilisez pas d'instruction if.

Dans les prochaines sections, nous écrirons deux fonctions qui additionnent des valeurs temporelles. Elles exemplifient deux types de fonctions : les fonctions pures et les modificateurs. Elles illustrent également un modèle de développement que j'appellerai prototypage et correction, dont l'objectif est d'aborder un problème complexe en commençant par un simple prototype et en traitant les difficultés de façon incrémentielle.

Voici un prototype simple de ajouter_temps :

def ajouter_temps(t1, t2):
    somme = Temps()
    somme.heure = t1.heure + t2.heure
    somme.minute = t1.minute + t2.minute
    somme.seconde = t1.seconde + t2.seconde
    return somme

La fonction crée un nouvel objet Temps, initialise ses attributs et renvoie une référence au nouvel objet. Cela s'appelle une fonction pure, car elle ne modifie aucun des objets qui lui sont passés comme arguments et elle n'a aucun effet, comme l'affichage d'une valeur ou l'obtention des données saisies par l'utilisateur, autre que de renvoyer une valeur.

Pour tester cette fonction, je vais créer deux objets Temps : debut contient l'heure de début d'un film, comme Monty Python : Sacré Graal !, et duree contient la durée du film, qui est d'une heure 35 minutes.

ajouter_temps calcule quand le film sera fini.

>>> debut = Temps()
>>> debut.heure = 9
>>> debut.minute = 45
>>> debut.seconde = 0

>>> duree = Temps()
>>> duree.heure = 1
>>> duree.minute = 35
>>> duree.seconde = 0

>>> fini = ajouter_temps(debut, duree)
>>> afficher_temps(fini)
10:80:00

Le résultat, 10:80:00 n'est peut-être pas ce que vous espériez. Le problème est que cette fonction ne traite pas les cas où le nombre de secondes ou de minutes additionnées dépasse soixante. Lorsque cela se produit, nous devons « retenir » ou « reporter » les secondes supplémentaires dans la colonne des minutes ou les minutes supplémentaires dans la colonne des heures.

Voici une version améliorée :

def ajouter_temps(t1, t2):
    somme = Temps()
    somme.heure = t1.heure + t2.heure
    somme.minute = t1.minute + t2.minute
    somme.seconde = t1.seconde + t2.seconde

    if somme.seconde >= 60:
        somme.seconde -= 60
        somme.minute += 1

    if somme.minute >= 60:
        somme.minute -= 60
        somme.heure += 1

    return somme

Bien que cette fonction soit correcte, elle commence à beaucoup grossir. Nous verrons plus tard une version plus courte.

Parfois, il est utile qu'une fonction puisse modifier les objets qu'elle reçoit comme paramètres. Dans ce cas, les changements sont visibles par la procédure appelante. Ce genre de fonctions s'appellent modificateurs.

incremente, qui ajoute un nombre donné de secondes à un objet Temps, peut être écrite naturellement comme un modificateur. Voici un premier jet :

def incremente(temps, secondes):
    temps.seconde += secondes

    if temps.seconde >= 60:
        temps.seconde -= 60
        temps.minute += 1

    if temps.minute >= 60:
        temps.minute -= 60
        temps.heure += 1

La première ligne effectue l'opération d'addition ; le reste traite les cas particuliers que nous avons vus dans la section précédente.

Cette fonction est-elle correcte ? Qu'advient-il si secondes est beaucoup plus élevé que soixante ?

Dans ce cas, il ne suffit pas de faire la retenue une seule fois ; nous devons continuer à la faire jusqu'à ce que la valeur temps.seconde soit inférieure à soixante. Une solution consiste à remplacer les instructions if par des instructions while. Cela rendrait la fonction correcte, mais pas très efficace. À titre d'exercice, écrivez une version correcte de incremente ne contenant aucune boucle.

Tout ce qui peut être fait avec des modificateurs peut également être fait avec des fonctions pures. En fait, certains langages de programmation dits « fonctionnels » autorisent uniquement les fonctions pures. Il existe certaines indications que les programmes qui utilisent des fonctions pures sont plus rapides à développer et moins sujets aux erreurs que les programmes qui utilisent des modificateurs. Mais les modificateurs sont commodes parfois, et les programmes fonctionnels ont tendance à être moins efficaces.

En général, je vous conseille d'écrire des fonctions pures chaque fois que cela est raisonnable et de recourir à des modificateurs uniquement si cela présente un avantage convaincant. Cette approche pourrait s'appeler un style fonctionnel de programmation.

À titre d'exercice, écrivez une version « pure » de incremente, qui crée et retourne un nouvel objet Temps plutôt que de modifier le paramètre.

Le modèle de développement que j'illustre ici s'appelle « prototypage et correction ». Pour chaque fonction, j'ai écrit un prototype qui effectue le calcul de base et ensuite je l'ai testé, en corrigeant les erreurs en chemin.

Cette approche peut être efficace, surtout si vous n'avez pas encore une compréhension profonde du problème. Mais les corrections incrémentales peuvent générer du code qui est inutilement compliqué - car il traite de nombreux cas spéciaux - et non fiable - car il est difficile de savoir si vous avez trouvé toutes les erreurs.

Une autre possibilité est le développement par conception, dans lequel une compréhension de haut niveau du problème peut rendre la programmation beaucoup plus facile. Dans ce cas, il s'agit de comprendre qu'un objet Temps est en fait un nombre à trois chiffres exprimés en base 60 (voir https://fr.wikipedia.org/wiki/Syst%C3%A8me_sexag%C3%A9simal) ! L'attribut seconde est la « colonne des unités », l'attribut minute est « la colonne des soixantaines », et l'attribut heure est « la colonne des trois mille six cents ».

Lorsque nous avons écrit ajouter_temps et increment, nous étions effectivement en train de faire des additions en base 60, ce qui explique pourquoi nous avons dû faire des retenues d'une colonne à l'autre.

Cette observation suggère une autre approche de l'ensemble du problème - nous pouvons convertir des objets Temps en entiers et profiter du fait que l'ordinateur sait comment faire l'arithmétique avec des entiers.

Voici une fonction qui convertit des Temps en entiers :

def temps_vers_int(temps):
    minutes = temps.heure * 60 + temps.minute
    secondes = minutes * 60 + temps.seconde
    return secondes

Et voici une fonction qui convertit un nombre entier vers un Temps (rappelez-vous que divmod effectue une division entière du premier argument par le second et renvoie le quotient et le reste sous la forme d'un tuple).

def int_vers_temps(secondes):
    temps = Temps()
    minutes, temps.seconde = divmod(secondes, 60)
    temps.heure, temps.minute = divmod(minutes, 60)
    return temps

Vous avez peut-être dû réfléchir un peu et exécuter quelques tests pour vous convaincre que ces fonctions sont correctes. Une façon de les tester est de vérifier que temps_vers_int(int_vers_temps(x)) == x pour de nombreuses valeurs de x. Cela représente un exemple d'un contrôle de cohérence.

Une fois que vous êtes convaincu qu'elles sont correctes, vous pouvez les utiliser pour réécrire ajouter_temps :

def ajouter_temps(t1, t2):
    secondes = temps_vers_int(t1) + temps_vers_int(t2)
    return int_vers_temps(seconds)

Cette version est plus courte que l'original, et plus facile à vérifier. À titre d'exercice, réécrivez incremente en utilisant temps_vers_int et int_vers_temps.

À certains égards, les conversions de base 60 à base 10 et vice-versa sont plus difficiles que le simple traitement des temps. La conversion de base est plus abstraite ; notre intuition pour traiter les valeurs de temps est meilleure.

Mais si nous avons l'intuition de traiter le temps comme un nombre en base 60 et nous faisons l'investissement d'écrire les fonctions de conversion (temps_vers_int et int_vers_temps), nous obtenons un programme qui est plus court, plus facile à lire et à déboguer, et plus fiable.

Il est également plus facile d'ajouter des fonctionnalités plus tard. Par exemple, imaginez la soustraction de deux Temps pour trouver la durée écoulée entre eux. L'approche naïve serait de mettre en œuvre la soustraction avec retenue. L'utilisation des fonctions de conversion serait plus facile et plus susceptible d'être correcte.

Ironie du sort, parfois le fait de rendre un problème plus difficile (ou plus général) le rend plus facile (car il y a moins de cas particuliers et moins de possibilités d'erreur).

Un objet Temps est bien formé si les valeurs de minute et seconde sont entre 0 et 60 (0 compris, mais 60 non compris) et si heure est positive. heure et minute doivent être des valeurs entières, mais nous pourrions permettre à seconde d'avoir une partie fractionnaire.

De telles exigences s'appellent des invariants, parce qu'elles doivent toujours être satisfaites. Autrement dit, si elles ne sont pas vraies, quelque chose a mal tourné.

Écrire du code pour vérifier les invariants peut aider à détecter les erreurs et à trouver leurs causes. Par exemple, vous pourriez avoir une fonction comme valider_temps qui prend un objet Temps et renvoie False si elle enfreint un invariant :

def valide_temps(temps):
    if temps.heure < 0 or temps.minute < 0 or temps.seconde < 0:
        return False
    if temps.minute >= 60 or temps.seconde >= 60:
        return False
    return True

Au début de chaque fonction, vous pourriez vérifier les arguments pour vous assurer qu'ils sont valides :

def ajouter_temps(t1, t2):
    if not valide_temps(t1) or not valide_temps(t2):
        raise ValueError('objet Temps invalide dans ajouter_temps')
    secondes = temps_vers_int(t1) + temps_vers_int(t2)
    return int_vers_temps(secondes)

Ou vous pouvez utiliser une instruction assert, qui vérifie un invariant donné et déclenche une exception si elle échoue :

def ajouter_temps(t1, t2):
    assert valide_temps(t1) and valide_temps(t2)
    secondes = temps_vers_int(t1) + temps_vers_int(t2)
    return int_vers_temps(secondes)

Les instructions assert sont utiles, car elles font la distinction entre un code qui traite des conditions normales et un code qui détecte les erreurs.

• prototypage et correction : un modèle de développement qui consiste à écrire un brouillon d'un programme, à tester et à corriger les erreurs trouvées.
• développement par conception : un modèle de développement qui implique une compréhension de haut niveau du problème et plus de planification que du développement incrémental ou du développement de prototypage.
• fonction pure : une fonction qui ne modifie pas les objets qu'elle reçoit comme arguments. La plupart des fonctions pures sont productives.
• modificateur : une fonction qui modifie un ou plusieurs objets qu'elle reçoit comme arguments. La plupart des modificateurs sont vides ; c'est-à-dire ils renvoient None.
• style fonctionnel de programmation : un style de conception de programmes dans lequel la majorité des fonctions sont pures.
• invariant : une condition qui doit toujours être vraie pendant l'exécution d'un programme.
• instruction assert : une instruction que vérifie une condition et déclenche une exception si elle échoue.

Exercice 1

Écrivez une fonction appelée mul_time qui prend un objet Temps et un nombre et retourne un nouvel objet Temps , qui contient le produit entre le Temps d'origine et le nombre.

Ensuite, utilisez mul_time pour écrire une fonction qui prend un objet Temps qui représente le temps de l'arrivée dans une course, et un nombre qui représente la distance, et retourne un objet Temps qui représente le rythme moyen (temps par kilomètre).

Exercice 2

Le module datetime fournit des objets time qui sont similaires aux objets Temps de ce chapitre, mais ils fournissent un riche ensemble de méthodes et d'opérateurs. Lisez-en la documentation à l'adresse http://docs.python.org/3/library/datetime.html.

1. Utilisez le module datetime pour écrire un programme qui prend la date actuelle et affiche le jour de la semaine.
2. Écrivez un programme qui prend en entrée un anniversaire et affiche l'âge de l'utilisateur et le nombre de jours, heures, minutes et secondes jusqu'à son prochain anniversaire.
3. Si deux personnes sont nées deux jours différents, il existe un jour où l'une d'entre elles est deux fois plus âgée que l'autre. C'est leur Jour double. Écrivez un programme qui prend deux dates de naissance et calcule leur Jour double.
4. Pour pimenter un peu le défi, écrivez la version plus générale qui calcule le jour où l'une des personnes est n fois plus âgée que l'autre.

Solution à l'adresse Time1_soln.py. Pour fonctionner, le code proposé ici nécessite la présence du fichier Time1.py contenant le code des programmes de ce chapitre (lien fourni en début de chapitre).