Pensez en Python

Supposons que vous ayez analysé deux algorithmes et estimé leur durée d'exécution en fonction de la taille n des données en entrée : l'Algorithme A nécessite 100 n + 1 étapes, et l'Algorithme B n² + n + 1 étapes.

Le tableau suivant illustre la durée d'exécution de ces algorithmes pour différentes tailles de données en entrée :

Pour une taille des données de n = 10, l'Algorithme A paraît très mauvais : il prend presque dix fois plus de temps que l'Algorithme B. Mais pour n = 100, les deux algorithmes se valent à peu près, et, pour des tailles plus grandes, A est bien meilleur que B. La raison fondamentale est que pour des valeurs élevées de n, toute fonction qui contient un terme en n² croîtra plus rapidement qu'une fonction dont le terme dominant est n. Le terme dominant est le terme de degré le plus élevé (c'est-à-dire celui qui contient l'exposant le plus grand).

Pour l'Algorithme A, le terme dominant a un coefficient assez élevé, 100, ce qui explique pourquoi B est meilleur que A pour des valeurs faibles de n. Cependant, quels que soient les coefficients a et b choisis, il y aura toujours des valeurs de n suffisamment grandes pour lesquelles an² > bn.

Il en va de même avec les termes non dominants. Même si le temps d'exécution de l'Algorithme A était de n + 1 000 000, celui-ci serait tout de même meilleur que l'Algorithme B pour des valeurs suffisamment grandes de n.

En termes mathématiques, on s'intéresse ici en quelque sorte au comportement asymptotique de la fonction représentant le temps d'exécution d'un algorithme quand n prend des valeurs très grandes ; ainsi, le tableau ci-dessus reflète le fait que la limite d'une fonction polynomiale, quand sa variable tend vers l'infini, dépend du terme dominant. D'une façon générale, nous attendons que l'algorithme ayant le plus petit terme dominant soit le meilleur pour les grands problèmes, mais, pour les problèmes plus petits, il se peut qu'il y ait un point de croisement (ou point de changement de méthode) en dessous duquel un autre algorithme est meilleur. L'endroit où se situe ce point de croisement dépend des détails des algorithmes, des données en entrée et du matériel, si bien qu'on l'ignore généralement dans le cadre de l'analyse algorithmique. Mais cela ne signifie pas que vous deviez l'oublier complètement.

Si deux algorithmes ont des termes dominants du même ordre (même exposant), alors il est difficile de dire lequel est le meilleur ; une nouvelle fois, la réponse dépendra des détails. Du coup, du point de vue de l'analyse algorithmique, des fonctions ayant des termes dominants du même ordre sont considérées comme équivalentes, même s'ils ont des coefficients différents.

Un ordre de croissance est un ensemble de fonctions ayant un type de croissance équivalent ou considéré comme tel. Par exemple, 2n, 100n et n+1 appartiennent au même ordre de croissance, que l'on note O(n) dans la « notation asymptotique en O » et que l'on appelle souvent linéaire, parce que toutes les fonctions de cet ensemble croissent linéairement en fonction de n. (À noter que le symbole « O » employé dans cette notation est la lettre « o » majuscule - on dit parfois aussi que c'est la lettre grecque omicron majuscule, qui s'écrit généralement de la même façon, « O » - mais pas le chiffre zéro 0 ; et O(n) se prononce habituellement « o de n » ou « grand o de n » [NdT].)

Toutes les fonctions dont le terme dominant est en n² appartiennent à O(n²). On les appelle quadratiques.

Le tableau suivant énumère quelques-uns des ordres de croissance les plus communément employés en analyse algorithmique, classés des meilleurs vers les pires :

Pour les termes logarithmiques, la base du logarithme n'importe pas : changer de base équivaut à multiplier par une constante, ce qui ne change pas l'ordre de croissance. De la même façon, toutes les fonctions exponentielles appartiennent au même ordre de croissance, indépendamment de la base de l'exposant. Les fonctions exponentielles (et factorielles) croissent extrêmement rapidement, si bien que ces fonctions ne sont utiles dans la pratique que pour des problèmes très petits.

Exercice 1.

Lisez la page Wikipédia sur la Comparaison algorithmique ( https://fr.wikipedia.org/wiki/Comparaison_asymptotique ), en complétant si possible avec la page équivalente en anglais ( https://en.wikipedia.org/wiki/Big_O_notation ), et répondez aux questions suivantes :

1. Quel est l'ordre de croissance de n³ + n² ? Et de 1 000 000 n³ + n² ? Et de n³ +1 000 000  n² ?
2. Quel est l'ordre de croissance de (n² + n) . (n + 1) ? Avant de commencer à faire les multiplications, rappelez-vous que vous n'avez besoin que du terme dominant.
3. Si la fonction f est en O(g), pour une fonction g non spécifiée, que pouvez-vous dire de l'ordre de croissance de f + b (b étant une constante) ?
4. Si les fonctions f1 et f2 sont en O(g), que pouvez-vous dire de f1 + f2 ?
5. Si f1 est en O(g) et f2 en O(h), que pouvez-vous dire de f1 + f2 ?
6. Si f1 est en O(g) et f2 en O(h), que pouvez-vous dire de f1 . f2 ?

Les programmeurs qui s'intéressent aux performances trouvent souvent ce genre d'analyse difficile à avaler. Ils n'ont pas complètement tort : parfois, les coefficients et les termes non dominants font une vraie différence. Parfois, les détails du matériel utilisé, le langage de programmation employé et les caractéristiques des données en entrée font une grosse différence. Et, pour les petits problèmes, le comportement asymptotique est sans importance.

Mais si vous gardez à l'esprit ces mises en garde relatives aux cas particuliers, l'analyse algorithmique est un outil utile. Au moins en ce qui concerne les problèmes de grande dimension, les algorithmes « meilleurs » du point de vue de cette analyse sont effectivement meilleurs, et parfois très largement meilleurs. La différence entre deux algorithmes ayant le même ordre de croissance est généralement un facteur à peu près constant, mais la différence entre un bon algorithme et un mauvais algorithme est sans limites !

En Python, la plupart des opérations arithmétiques prennent un temps constant ; la multiplication prend plus de temps que l'addition et la soustraction, et la division en prend encore un peu plus, mais ces durées d'exécution ne dépendent pas de la taille des opérandes. Il y a cependant une exception pour les très très grands entiers : dans ce cas, la durée d'exécution croît avec le nombre de chiffres.

Les opérations d'indexation - lire ou écrire des éléments d'une séquence ou d'un dictionnaire - prennent également un temps constant, indépendant de la taille de la structure de donnée.

Une boucle for qui parcourt une séquence ou un dictionnaire a une complexité linéaire, à condition que toutes les opérations effectuées dans le corps de la boucle soient en complexité constante. Par exemple, accumuler les éléments d'une liste est une opération linéaire :

total = 0
for x in t:
    total += x

La fonction interne sum est également linéaire, car elle fait la même chose, mais elle tend à être plus rapide parce qu'elle bénéficie d'une implémentation plus efficace ; en termes d'analyse algorithmique, le coefficient de son terme dominant est plus petit.

En règle générale, si le corps d'une boucle est en O(n^a), dans le cas par exemple d'une boucle imbriquée, alors l'ensemble de la boucle est en O(n^a+1). Il y a une exception si vous pouvez établir que la boucle sort après un nombre constant d'itérations. Si la boucle s'exécute k fois indépendamment de la valeur de n, alors la boucle restera en O(n^a), même si k est grand.

Multiplier par k ne modifie par l'ordre de croissance, mais diviser par k ne le fait pas non plus. Donc, si le corps d'une fonction est en O(n^a) et qu'elle s'exécute n/k fois, alors l'ensemble de la boucle est en O(n^a+1), même si k est grand.

La plupart des opérations sur les chaînes de caractères et les tuples sont linéaires, à l'exception des opérations d'indexation et de len, qui sont en temps constant. Les fonctions internes min et max sont linéaires. La durée d'exécution d'une opération de tranche est proportionnelle au nombre des valeurs renvoyées, mais indépendante de la taille des données en entrée.

Les concaténations de chaînes sont linéaires ; la durée d'exécution dépend de la somme des longueurs des opérandes.

Toutes les méthodes de chaînes sont linéaires, mais, si les longueurs des chaînes sont plafonnées par une constante - par exemple si les opérations portent sur des caractères uniques - alors elles sont considérées comme étant en temps constant. La méthode de chaîne join est linéaire ; la durée d'exécution dépend de la longueur totale des chaînes.

La plupart des méthodes de listes sont linéaires, mais il y a des exceptions :

• ajouter un élément à la fin d'une liste est en temps constant en moyenne ; quand l'opération manque de place, la liste est occasionnellement copiée dans un emplacement plus grand, mais, globalement, la durée d'exécution pour n ajouts est en O(n), si bien que la durée moyenne est en O(1) ;
• retirer un élément de la fin d'une liste est en temps constant ;
• trier une liste avec les fonctions de tri Python est en O(n log n).

La plupart des opérations et méthodes relatives aux dictionnaires sont en temps constant, mais il y a quelques exceptions :

• la durée d'exécution d'une mise à jour est proportionnelle au volume des données à mettre à jour, mais indépendante de la taille du dictionnaire à mettre à jour ;
• les fonctions keys, values et items sont en temps constant, car elles renvoient des itérateurs. Mais si vous bouclez sur ces itérateurs, la boucle sera linéaire.

Les performances affichées par les dictionnaires sont l'un des petits miracles de l'informatique. Nous étudierons comment ils fonctionnent dans la section B.4Tables de hachage.

Exercice 2

Lisez la page Wikipédia sur les algorithmes de tri ( https://fr.wikipedia.org/wiki/Algorithme_de_tri#Classification ) et répondez aux questions suivantes :

1. Qu'est-ce qu'un « tri par comparaisons » ? Quel est le meilleur ordre de croissance dans le pire des cas pour un tri par comparaison ?
2. Quel est l'ordre de croissance du tri à bulles, et pourquoi Barak Obama pense-t-il que c'est un mauvais choix ?
3. Quel est l'ordre de croissance du tri par base (radix sort) ? Quelles sont les conditions préalables à son utilisation ?
4. Qu'est-ce qu'un tri stable et pourquoi la stabilité peut-elle avoir de l'importance en pratique ?
5. Quel est le pire algorithme de tri (parmi ceux énumérés) ?
6. Quel algorithme de tri utilise la bibliothèque C ? Quel est l'algorithme de tri utilisé par Python ? Ces algorithmes sont-ils stables ? Il se peut que vous deviez faire quelques recherches sur Google pour répondre à ces questions.
7. Beaucoup des algorithmes qui ne sont pas des tris par comparaisons sont linéaires. Mais alors, pourquoi Python utilise-t-il un algorithme de tri par comparaisons en O(n log n) ?

Un algorithme de recherche est un algorithme qui prend en entrée une liste d'éléments et un élément cible à rechercher dans cette collection, et renvoie souvent la position ou l'indice de la cible.

L'algorithme de recherche le plus simple est celui de la « recherche linéaire », qui parcourt les éléments de la liste en entrée dans l'ordre et s'arrête s'il trouve la cible. Dans le pire des cas, il doit parcourir toute la liste, et la durée d'exécution est donc linéaire.

L'opérateur de séquences in emploie une recherche linéaire, de même que les méthodes find et count.

Si les éléments de la séquence sont ordonnés, alors vous pouvez utiliser une recherche dichotomique, qui est en O(log n). Une recherche par dichotomie est analogue à la méthode que vous utilisez probablement très naturellement pour trouver un numéro de téléphone dans un annuaire téléphonique : au lieu de commencer à lire les éléments un par un depuis le début, vous commencez à peu près au milieu et vérifiez si le nom que vous cherchez est avant ou après. S'il vient avant, vous cherchez dans la première moitié, sinon dans la seconde moitié. Dans un cas comme dans l'autre, vous divisez de moitié le nombre d'éléments restants. Et vous recommencez à diviser en deux la moitié que vous avez sélectionnée, et ainsi de suite jusqu'au succès (ou jusqu'à l'échec si l'élément recherché ne figure pas dans la liste).

Si la séquence possède 1 000 000 éléments, il faudra environ 20 étapes (dans le pire des cas) pour trouver l'élément recherché ou conclure qu'il n'est pas là. Cette méthode est donc, pour un million d'éléments, environ 50 000 fois plus rapide qu'une recherche linéaire.

La recherche dichotomique peut être beaucoup plus rapide qu'une recherche linéaire, mais il faut que la séquence soit ordonnée, ce qui peut nécessiter du travail supplémentaire.

Il existe une autre structure de données, nommée table de hachage, qui est plus rapide encore - elle peut effectuer une recherche en temps constant - et ne nécessite pas de trier les données. Les dictionnaires de Python sont implémentés avec des tables de hachage, et c'est la raison pour laquelle la plupart des opérations sur les dictionnaires, notamment l'opérateur in, sont en temps constant.

Pour expliquer comment fonctionnent les tables de hachage et pourquoi leurs performances sont si bonnes, je vais commencer à coder une simple table de correspondance et l'améliorer progressivement jusqu'à arriver à une table de hachage.

J'utilise Python pour illustrer cette implémentation, mais, dans la vie réelle, vous n'auriez pas besoin d'écrire ce genre de code en Python : vous utiliseriez simplement un dictionnaire ! Donc, pour le reste de cette section, imaginez que les dictionnaires n'existent pas en Python et que vous vouliez mettre en œuvre une structure de données établissant une correspondance entre des clés et des valeurs. Les opérations que vous avez besoin de développer sont les suivantes :

• ajoute(c, v) : ajoute un nouvel élément faisant correspondre une clé c à une valeur v. Avec un dictionnaire Python nommé dict, cette opération s'écrirait dict[c] = v.
• cherche(c) : fait une recherche et renvoie la valeur correspondant à la clé c. Avec un dictionnaire Python nommé dict, cette opération s'écrirait dict[k] ou dict.get(c).

Supposons pour l'instant que chaque clé n'apparaît qu'une seule fois. La façon la plus simple de réaliser une telle table de correspondance est d'utiliser une liste de tuples, dans laquelle chaque tuple est une paire clé-valeur.

class CorrespondanceLineaire:

    def __init__(self):
        self.items = []

    def ajoute(self, c, v):
        self.items.append((c, v))

    def cherche(self, c):
        for clef, valeur in self.items:
            if clef == c:
                return valeur
        raise KeyError

La méthode ajoute insère un tuple clé-valeur à la fin de la liste d'éléments.

La méthode cherche utilise une boucle for pour parcourir la liste ; si elle trouve la clé recherchée, elle renvoie la valeur correspondante ; sinon, elle renvoie une exception KeyError. Cette méthode de recherche est linéaire, en O(n).

Une autre solution serait de maintenir la liste triée par clé. Nous pourrions alors employer une recherche dichotomique, qui est en O(log n). La recherche serait plus rapide, mais insérer un nouvel élément au milieu d'une liste est linéaire, ce n'est donc sans doute pas la meilleure solution. Il y a d'autres structures de données qui peuvent implémenter les opérations ajoute et cherche en des temps logarithmiques, mais ce n'est toujours pas aussi bien qu'un temps constant, donc cherchons d'autres solutions.

Une façon d'améliorer CorrespondanceLineaire est de diviser la liste de paires clé-valeur en listes plus petites. Voici une implémentation baptisée MeilleureCorrespondance, qui est une liste de 100 exemplaires de CorrespondanceLinéaire que nous appellerons godets. Comme nous le verrons dans un instant, l'ordre de croissance de cherche est toujours linéaire, mais MeilleureCorrespondance est un grand pas en direction des tables de hachage.

class MeilleureCorrespondance:

    def __init__(self, n=100):
        self.godets = []
        for i in range(n):
            self.godets.append(CorrespondanceLineaire())

    def trouve_godet(self, c):
        indice = hash(c) % len(self.godets)
        return self.godets[indice]

    def ajoute(self, c, v):
        m = self.trouve_godet(c)
        m.ajoute(k, v)

    def cherche(self, c):
        m = self.trouve_godet(c)
        return m.get(c)

La méthode __init__ crée une liste de n godets de type CorrespondancesLineaire.

La méthode trouve_godet est utilisée par ajoute et cherche pour déterminer dans quel godet mettre le nouvel élément, ou dans quel godet aller chercher un élément.

La méthode trouve_godet utilise la fonction interne hash de Python, une fonction de hachage qui prend en entrée un objet Python presque quelconque et renvoie un entier. Cette implémentation présente un défaut : elle ne fonctionne qu'avec des clés hachables. Les types mutables comme les listes et les dictionnaires ne sont pas hachables.

Les objets hachables qui sont considérés comme équivalents renvoient la même valeur de hachage, mais l'inverse n'est pas nécessairement vrai : deux objets ayant des valeurs différentes peuvent renvoyer la même valeur de hachage.

La méthode trouve_godet utilise l'opérateur modulo pour réduire les valeurs de hachage à un intervalle compris entre 0 et len(self.godets), en sorte que le résultat soit un indice valide de la liste. Bien entendu, ceci signifie que nombreuses valeurs de hachage seront réduites au même indice. Mais si la fonction de hachage répartit les choses de façon à peu près uniforme (les fonctions de hachages sont conçues pour cela), alors nous pouvons nous attendre à environ n/100 éléments par CorrespondanceLineaire.

Puisque la durée d'exécution de CorrespondanceLineaire.cherche est proportionnelle au nombre d'éléments, nous pouvons espérer que MeilleureCorrespondance sera environ 100 fois plus rapide que CorrespondanceLineaire. L'ordre de croissance est toujours linéaire, mais les coefficients dominants sont beaucoup plus petits. C'est bien, l'amélioration est spectaculaire, mais ce n'est toujours pas aussi bien qu'une table de hachage.

Voici (finalement) l'idée cruciale qui rend si rapides les tables de hachages : si vous parvenez à maintenir la longueur des godets CorrespondanceLinéaire en dessous d'une certaine limite maximale, alors la méthode CorrespondanceLineaire.cherche est en temps constant. Il vous suffit de garder en mémoire le nombre d'éléments et, quand ce nombre par godet CorrespondanceLinéaire dépasse un certain seuil, de redimensionner la table de hachage en ajoutant de nouveaux godets.

Voici une mise en œuvre d'une table de hachage :

class Hachage:

    def __init__(self):
        self.godets = MeilleureCorrespondance(2)
        self.num = 0

    def trouve(self, c):
        return self.godets.trouve(c)

    def ajoute(self, c, v):
        if self.num == len(self.maps.maps):
            self.resize()
        self.godets.ajoute(c, v)
        self.num += 1

    def redimensionne(self):
        nouveaux_godets = MeilleureCorrespondance(self.num * 2)
        for m in self.godets.godets:
            for c, v in m.items:
                nouveaux_godets.ajoute(c, v)
        self.godets = nouveaux_godets

Chaque Hachage contient un MeilleureCorrespondance ; __init__ commence avec deux MeilleureCorrespondance et initialise num qui garde le décompte du nombre d'éléments.

La méthode get retransmet les invocations à MeilleureCorrespondance. Le vrai travail a lieu dans ajoute, qui vérifie le nombre d'éléments et la taille de MeilleureCorrespondance ; s'ils sont égaux, le nombre moyen d'éléments par CorrespondanceLinéaire est 1, elle appelle redimensionne.

La méthode redimensionne crée un nouvel objet MeilleureCorrespondance, deux fois plus grand que le précédent, et « rehache » ensuite les éléments du vieux godet dans le nouveau.

Le rehachage est nécessaire parce que changer le nombre de CorrespondanceLinéaire modifie le dénominateur de l'opérateur modulo dans trouve_godet. Ce qui veut dire que certains objets qui étaient hachés dans le même CorrespondanceLinéaire vont être répartis ailleurs (et c'est exactement le but recherché, n'est-ce pas?).

Le rehachage est en temps linéaire, si bien que redimensionne sera linéaire, ce qui peut paraître mauvais, puisque j'ai promis que la méthode ajoute serait en temps constant. Mais rappelez-vous que nous ne devons pas rehacher à chaque fois, si bien qu'ajoute est habituellement en temps constant, et seulement occasionnellement linéaire. La quantité totale de travail requise pour ajouter n fois est proportionnelle à n, si bien que la durée moyenne de chaque ajout est en temps constant !

Pour voir comment ça marche, considérons que nous commençons avec un hachage vide et y ajoutons ensuite une séquence d'éléments. Nous commençons avec deux godets CorrespondanceLinéaire, les deux premiers ajouts sont donc rapides (pas de redimensionnement). Disons qu'ils consomment chacun une unité de travail. L'ajout suivant nécessite un redimensionnement, donc nous devons rehacher les deux premiers éléments (disons que cela représente deux unités de travail) et ajouter ensuite le troisième élément (une unité de travail de plus). Ajouter l'élément suivant coûte une unité, donc nous en sommes pour l'instant à 6 unités de travail pour 4 éléments.

L'ajout suivant coûte 5 unités, mais les trois ajouts suivants ne coûtent qu'une unité chacun, donc nous en arrivons à 14 unités pour les 8 premiers ajouts.

L'ajout suivant coûte 9 unités, mais nous pouvons maintenant ajouter 7 éléments supplémentaires au prix d'une unité chacun ; au total, nous en sommes à 30 unités pour les 16 premiers ajouts.

Après 32 ajouts, le coût total est de 62 unités, et j'espère que vous commencez à voir ce qui se passe. Après n ajouts, n étant une puissance de deux, le coût total est de 2n - 2 unités, si bien que le travail moyen par ajout est d'un peu moins de 2 unités. Le cas est optimal quand n est une puissance de deux, et le travail moyen est un peu plus élevé pour d'autres valeurs de n, mais cela importe peu. La chose importante est que nous sommes en O(1).

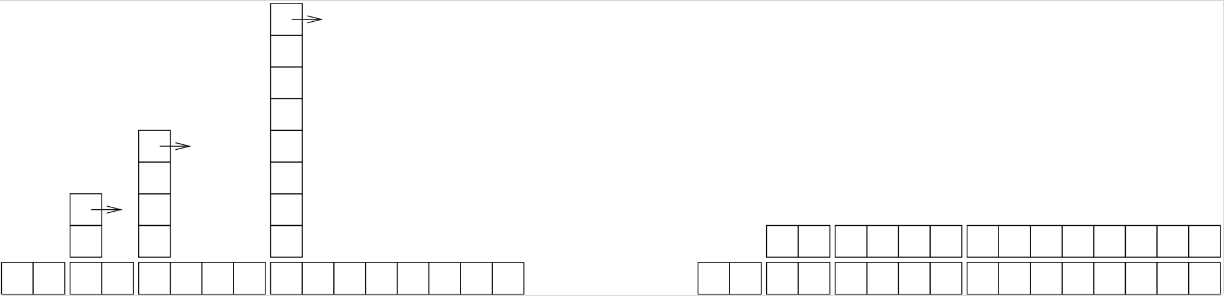
La figure B.1 illustre ce processus graphiquement. Chaque bloc représente une unité de travail. Les colonnes représentent le travail total pour chaque ajout, dans l'ordre, de gauche à droite : les deux premiers ajouts coûtent une unité, le troisième 3 unités, et ainsi de suite.

Le travail de rehachage se présente comme une suite de « tours » de plus en plus hautes, avec des intervalles de plus en plus grands entre elles. Mais si vous faites basculer les tours vers la droite, afin de répartir le coût des redimensionnements sur l'ensemble des ajouts s'y rapportant, vous pouvez voir graphiquement que le coût total après n ajouts est de 2n - 2.

Une caractéristique essentielle de cet algorithme est que, quand on redimensionne le hachage, il croît géométriquement, ce qui veut dire que l'on multiplie la taille par une constante (2 dans notre exemple) à chaque étape. Si on avait décidé de faire croître la taille arithmétiquement, c'est-à-dire d'ajouter un nombre constant d'emplacements à chaque fois, alors la durée moyenne par ajout aurait été linéaire. C'est le choix de la croissance géométrique de la taille qui permet d'obtenir un ajout en temps constant.

Vous pouvez télécharger mon implémentation de ce hachage à l'adresse suivante : Map.py. Mais souvenez-vous qu'il n'y a aucune raison de l'utiliser à d'autres fins que l'expérimentation pédagogique ; si vous avez besoin de ce genre d'outils, utilisez tout simplement un dictionnaire Python.

• analyse algorithmique : une façon de comparer les algorithmes du point de vue de leur durée d'exécution et de leur besoin mémoire.
• modèle de machine : une représentation simplifiée d'un ordinateur utilisée pour décrire des algorithmes.
• terme dominant : dans un polynôme, le terme de plus haut degré (ayant l'exposant le plus grand).
• point de croisement : la taille du problème pour laquelle deux algorithmes nécessitent la même durée d'exécution ou la même empreinte mémoire.
• ordre de croissance : un ensemble de fonctions qui croissent toutes d'une façon considérée comme équivalente du point de vue de l'analyse algorithmique. Par exemple, toutes les fonctions qui croissent linéairement appartiennent au même ordre de croissance.
• notation asymptotique en O : notation permettant de représenter un ordre de croissance ; par exemple O(n) représente l'ensemble des fonctions qui croissent linéairement.
• quadratique : un algorithme dont la durée d'exécution est proportionnelle à n², n étant une mesure de la taille du problème.
• recherche : le problème consistant à trouver l'emplacement d'un élément dans une collection (par exemple une liste ou un dictionnaire) ou à conclure qu'il n'est pas présent.
• recherche par dichotomie : une méthode de recherche dans une liste ordonnée consistant à recherche un élément au milieu de la liste et à poursuivre la recherche dans la moitié de la liste susceptible de contenir l'élément cible, et ainsi de suite.
• table de hachage : une structure de données qui représente une collection de paires clé-valeur et permet d'effectuer des recherches en temps constant.