Pensez en Python

L'opérateur de division entière, //, divise un nombre par un autre et arrondit le résultat à l'entier juste en dessous. Par exemple, supposons que la durée d'un film est de 105 minutes. Vous voudrez peut-être savoir combien de temps cela fait en heures. La division classique retourne un nombre à virgule flottante :

>>> minutes = 105
>>> minutes / 60
1.75

Mais, généralement nous n'écrivons pas les heures avec décimales. La division entière renvoie le nombre entier d'heures, tronquant la partie fractionnaire :

>>> minutes = 105
>>> heures = minutes // 60
>>> heures
1

Pour obtenir le reste, vous devez soustraire une heure du total des minutes :

>>> reste = minutes - heures * 60
>>> reste
45

Une autre possibilité consiste à utiliser l'opérateur modulo, %, qui effectue la division et renvoie le reste.

>>> reste = minutes % 60
>>> reste
45

L'opérateur modulo est plus utile qu'il n'y paraît. Par exemple, vous pouvez vérifier si un nombre est divisible par un autre : si x % y est égal à zéro, alors x est divisible par y.

Vous pouvez aussi extraire les chiffres ou le chiffre le plus à droite d'un nombre. Par exemple, x % 10 donne le chiffre le plus à droite de x (en base 10). De même, x % 100 donne les deux derniers chiffres.

Si vous utilisez Python 2, la division fonctionne différemment. L'opérateur de division, /, effectue la division entière si les deux opérandes sont des nombres entiers, et la division décimale si l'un au moins des opérandes est un float.

Une expression booléenne est une expression qui est soit vraie, soit fausse. Les exemples suivants utilisent l'opérateur ==, qui compare deux opérandes et produit True (« vrai ») s'ils sont égaux et False (« faux ») sinon :

>>> 5 == 5
True
>>> 5 == 6
False

True et False sont des valeurs particulières qui appartiennent au type bool ; ce ne sont pas des chaînes de caractères :

>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>

L'opérateur == est l'un des opérateurs relationnels ; les autres sont :

x != y               # x n'est pas égal à y
x > y                # x est supérieur à y
x < y                # x est inférieur à y
x >= y               # x est supérieur ou égal à y
x <= y               # x est inférieur ou égal à y

Bien que ces opérations vous soient probablement familières, les symboles de Python sont différents des symboles mathématiques. Une erreur courante consiste à utiliser un seul signe égal (=) au lieu d'un signe égal double (==). Rappelez-vous que = est un opérateur d'affectation et == est un opérateur relationnel. Il n'existe pas d'opérateurs tels que =< ou =>.

Il y a trois opérateurs logiques : and, or, et not. La sémantique (le sens) de ces opérateurs est similaire à leur signification en anglais : « et », « ou » et respectivement « non ». Par exemple, l'expression x > 0 and x < 10 est vraie seulement si x est supérieur à 0 et inférieur à 10.

L'expression n % 2 == 0 or n % 3 == 0 est vraie si l'une ou les deux conditions est remplie, à savoir, si le nombre n est divisible par 2 ou par 3.

Enfin, l'opérateur not nie une expression booléenne, donc l'expression not (x > y) est vraie si x > y est fausse, c'est-à-dire, si x est inférieur ou égal à y.

Au sens strict, les opérandes des opérateurs logiques devraient être des expressions booléennes, mais Python n'est pas très strict. Tout nombre différent de zéro est interprété comme True :

>>> 42 and True
True

Cette souplesse peut être utile, mais il y a quelques subtilités qui pourraient être source de confusion. Vous avez peut-être intérêt à l'éviter (sauf si vous savez ce que vous faites).

Pour pouvoir écrire des programmes utiles, nous devons presque toujours vérifier les conditions et modifier le comportement du programme en conséquence. Les instructions conditionnelles nous donnent cette possibilité. La forme la plus simple est l'instruction if :

if x > 0:
    print('x est positif')

L'expression booléenne après if est appelée condition. Si elle est vraie, l'instruction indentée est exécutée. Sinon, rien ne se passe.

Les instructions if ont la même structure que les définitions de fonctions : un en-tête, suivi d'un corps indenté. Ce genre d'instructions sont appelées instructions composées.

Il n'y a aucune limite sur le nombre d'instructions qui peuvent apparaître dans le corps, mais il doit y en avoir au moins une. Parfois, il est utile d'avoir un corps sans instructions (généralement, pour réserver de la place pour du code que vous n'avez pas encore écrit). Dans ce cas, vous pouvez utiliser l'instruction pass, qui ne fait rien.

if x < 0:
    pass          # TODO: il faut gérer les valeurs négatives !

Une deuxième forme de l'instruction if est l'« exécution alternative », dans laquelle il y a deux possibilités et la condition détermine laquelle est exécutée. La syntaxe ressemble à ceci :

if x % 2 == 0:
    print('x est pair')
else:
    print('x est impair')

Si le reste de la division de x par 2 est égal à 0, alors nous savons que x est pair, et le programme affiche un message approprié. Si la condition est fausse, la deuxième série d'instructions est exécutée. Puisque la condition doit être soit vraie, soit fausse, une seule des branches de l'alternative sera exécutée. Les alternatives sont appelées branchement, parce qu'elles sont des branchements dans le flux d'exécution.

Parfois, il y a plus de deux possibilités et nous avons besoin de plus de deux branches. Une façon d'exprimer ce genre de calcul est un enchaînement de conditions :

if x < y:
    print('x plus petit que y')
elif x > y:
    print('x plus grand que y')
else:
    print('x et y sont égaux')

elif est une abréviation de « else if ». Ici encore, exactement une seule branche sera exécutée. Il n'y a aucune limite sur le nombre d'instructions elif. S'il existe une clause else, elle doit être à la fin, mais elle n'est pas obligatoire.

if choix == 'a':
    dessiner_a()
elif choix == 'b':
    dessiner_b()
elif choix == 'c':
    dessiner_c()

Chaque condition est vérifiée dans l'ordre. Si la première est fausse, la prochaine est vérifiée, et ainsi de suite. Si l'une d'entre elles est vraie, la branche correspondante est exécutée et l'instruction se termine. Même si plusieurs conditions sont vraies, seule la branche correspondant à la première condition vraie est exécutée.

Les structures conditionnelles peuvent également être imbriquées les unes dans les autres. Nous aurions pu écrire l'exemple de la section précédente comme ceci :

if x == y:
    print('x et y sont égaux')
else:
    if x < y:
        print('x est plus petit que y')
    else:
        print('x est plus grand que y')

La structure conditionnelle externe contient deux branches. La première branche contient une simple instruction. La seconde branche contient une autre instruction if, qui a deux branches à son tour. Ces deux branches sont de simples instructions, même si elles aussi auraient pu être des instructions conditionnelles.

Bien que l'indentation des instructions rende la structure apparente, les conditions imbriquées deviennent très rapidement difficiles à lire. Il est judicieux de les éviter quand c'est possible.

Les opérateurs logiques offrent souvent un moyen de simplifier les instructions conditionnelles imbriquées. Par exemple, le code suivant :

if 0 < x:
    if x < 10:
        print("x est un nombre positif d'un seul chiffre.")

peut se réécrire en utilisant une seule condition. L'instruction print est exécutée uniquement si les deux conditions sont vraies. Donc, nous pouvons obtenir le même effet en utilisant l'opérateur and :

if 0 < x and x < 10:
    print("x est un nombre positif d'un seul chiffre.")

Pour ce genre de condition, Python fournit une option plus concise :

if 0 < x < 10:
    print("x est un nombre positif d'un seul chiffre.")

Une fonction peut en appeler une autre ; il est également autorisé qu'une fonction s'appelle elle-même. Les avantages de ce genre de construction ne sont peut-être pas évidents, mais cela se révèle être l'une des choses les plus magiques qu'un programme puisse faire. Par exemple, considérez la fonction suivante :

def compte_a_rebours(n):
    if n <= 0:
        print('Décollez !')
    else:
        print(n)
        compte_a_rebours(n-1)

Si n est 0 ou négatif, elle affiche le mot « Décollez ! ». Sinon, elle affiche n et ensuite appelle une fonction nommée compte_a_rebours, elle-même, en passant n-1 comme argument.

Qu'advient-il si nous appelons cette fonction ainsi ?

>>> compte_a_rebours(3)

L'exécution de compte_a_rebours commence avec n = 3. Puisque n est supérieur à 0, elle affiche la valeur 3, puis s'appelle elle-même...

• L'exécution de compte_a_rebours commence avec n = 2, et puisque n est supérieur à 0, elle affiche la valeur 2, puis s'appelle elle-même...

  • L'exécution de compte_a_rebours commence avec n = 1, et puisque n est supérieur à 0, elle affiche la valeur 1, puis s'appelle elle-même...

    • L'exécution de compte_a_rebours commence avec n = 0, et puisque n n'est pas supérieur à 0, elle affiche le mot « Décollez ! », puis retourne.
  • La fonction compte_a_rebours qui a reçu la valeur n = 1 retourne.
• La fonction compte_a_rebours qui a reçu la valeur n = 2 retourne.

La fonction compte_a_rebours qui a reçu la valeur n = 3 retourne.

Vous êtes maintenant de retour dans __main__. En définitive, l'affichage ressemble à ceci :

3
2
1
Décollez !

Une fonction qui s'appelle elle-même est dite récursive ; le processus de son exécution est appelé récursivité.

Voici un autre exemple d'une fonction qui affiche une chaîne de caractères n fois.

def afficher_n(chaine, n):
    if n <= 0:
        return
    print(chaine)
    afficher_n(chaine, n-1)

Si n <= 0, l'instruction return fait sortir de la fonction. Le flux d'exécution retourne immédiatement à l'appelant, et les lignes suivantes de la fonction ne sont pas exécutées.

Le reste de la fonction est similaire à compte_a_rebours : elle affiche chaine et s'appelle elle-même pour afficher chaine encore n-1 fois. Ainsi, le nombre de lignes en sortie est 1 + (n - 1), ce qui donne n.

Pour des exemples simples de ce genre, il est probablement plus facile d'utiliser une boucle for. Mais nous verrons plus loin des exemples qui sont difficiles à écrire avec une boucle for et faciles à écrire avec la récursivité, il est donc bien de commencer tôt.

Dans la section 3.9Diagrammes de pile, nous avons utilisé un diagramme de pile pour représenter l'état d'un programme au cours d'un appel de fonction. Le même type de diagramme peut aider à interpréter une fonction récursive.

Chaque fois qu'une fonction est appelée, Python crée une structure de pile pour contenir les variables et les paramètres locaux de la fonction. Pour une fonction récursive, il se peut qu'il y ait plus d'une structure sur la pile en même temps.

La figure 5.1 représente un diagramme de pile pour compte_a_rebours appelée avec n = 3.

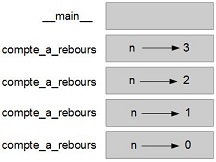
Comme d'habitude, le haut de la pile est la structure pour __main__. Il est vide parce que nous n'avons créé aucune variable dans __main__ et ne lui avons passé aucun argument.

Les quatre structures de compte_a_rebours ont des valeurs différentes pour le paramètre n. Le bas de la pile, là où n = 0, est appelé le cas de base. Il ne fait aucun appel récursif, donc il n'y a aucune autre structure après lui.

À titre d'exercice, dessinez un diagramme de pile pour afficher_n, appelée avec chaine = 'Hello' et n = 2. Ensuite, écrivez une fonction appelée faire_n, qui prend comme arguments un objet fonction et un nombre n, et qui appelle n fois la fonction passée en argument.

Si une cascade d'appels récursifs n'atteint jamais un cas de base, les appels récursifs se poursuivent pour l'éternité, et le programme ne se termine jamais. C'est ce que l'on appelle une récursion infinie, et ce n'est généralement pas une bonne idée. Voici un programme minimal avec une récursion infinie :

def recurse():
    recurse()

Dans la plupart des environnements de programmation, un programme avec une récursion infinie ne s'exécutera pas tout à fait éternellement. Python affiche un message d'erreur lorsque la profondeur maximale de récursivité est atteinte :

  File "<stdin>", line 2, in recurse
  File "<stdin>", line 2, in recurse
  File "<stdin>", line 2, in recurse
                  .   
                  .
                  .
  File "<stdin>", line 2, in recurse
  RuntimeError: Maximum recursion depth exceeded

Cette trace d'appel est un peu plus longue que celle que nous avons vue dans le chapitre précédent. Lorsque l'erreur se produit, il y a 1000 structures récursives sur la pile !

Si votre code génère par accident une récursion infinie, examinez votre fonction pour confirmer qu'il y a un scénario de base qui ne fait aucun appel récursif. Et s'il y a un cas de base, vérifiez si vous avez la garantie de l'atteindre.

Les programmes que nous avons écrits jusqu'ici n'acceptent aucune intervention de l'utilisateur. Ils font juste la même chose chaque fois.

Python fournit une fonction interne appelée input qui suspend l'exécution d'un programme et attend que l'utilisateur tape quelque chose au clavier. Lorsque l'utilisateur appuie sur la touche Retour ou Entrée, l'exécution du programme reprend et input renvoie une chaîne contenant ce que l'utilisateur a tapé. En Python 2, la même fonction est appelée raw_input.

>>> text = input()
Qu'est-ce que tu attends ?
>>> text
Qu'est-ce que tu attends ?

Avant d'obtenir les données saisies par l'utilisateur, il est souhaitable d'afficher une invite indiquant à l'utilisateur que taper. input peut prendre comme argument une invite :

>>> nom = input('Quel...est votre nom ?\n')
Quel...est votre nom ?
Arthur, Roi des Bretons !
>>> nom
Arthur, Roi des Bretons !

La séquence \n à la fin de l'invite représente un saut de ligne, qui est un caractère spécial qui provoque un passage à la ligne. Voilà pourquoi l'entrée de l'utilisateur apparaît à la ligne, en dessous de l'invite.

Si vous vous attendez à ce que l'utilisateur tape un nombre entier, vous pouvez essayer de convertir la valeur de retour en int :

>>> invite = 'À quelle vitesse vole une hirondelle égarée ?\n'
>>> vitesse = input(invite)
À quelle vitesse vole une hirondelle égarée ?
42
>>> int(vitesse)
42

Mais si l'utilisateur tape autre chose qu'une chaîne de chiffres, vous obtenez une erreur :

>>> vitesse = input(invite)
À quelle vitesse vole une hirondelle égarée ?
Vous voulez dire une hirondelle africaine ou européenne ?
>>> int(vitesse)
ValueError: invalid literal for int() with base 10

Nous verrons plus loin comment gérer ce genre d'erreur.

Lorsqu'une erreur de syntaxe ou d'exécution se produit, le message d'erreur contient beaucoup d'informations, mais on peut se retrouver dépassé. Les parties les plus utiles sont généralement :

• le genre d'erreur et
• l'endroit où elle est survenue.

Les erreurs de syntaxe sont généralement faciles à trouver, mais il y a quelques astuces. Les erreurs d'espace blanc peuvent être difficiles à repérer parce que les espaces et tabulations sont invisibles et nous sommes habitués à les ignorer.

>>> x = 5
>>>  y = 6
  File "<stdin>", line 1
    y = 6
    ^
IndentationError: unexpected indent

Dans cet exemple, le problème est que la deuxième ligne est en retrait d'un espace. Mais le message d'erreur indique y, ce qui est trompeur. En général, les messages d'erreur indiquent où le problème a été découvert, mais l'erreur réelle peut parfois se trouver plus haut dans le code, parfois sur une ligne précédente.

La même chose s'applique aux anomalies d'exécution. Supposons que vous essayez de calculer un rapport signal / bruit en décibels. La formule est Rapport signal/bruit = 10 log₁₀ (Psignal / Pbruit). En Python, vous pourriez essayer d'écrire quelque chose comme ceci :

import math
puissance_signal = 9
puissance_bruit = 10
ratio = puissance_signal // puissance_bruit
decibels = 10 * math.log10(ratio)
print(decibels)

Lorsque vous exécutez ce programme, vous obtenez une erreur :

Traceback (most recent call last):
  File "snr.py", line 5, in ?
    decibels = 10 * math.log10(ratio)
ValueError: math domain error

Le message indique une erreur ligne 5, mais il n'y a aucune erreur sur cette ligne. Pour trouver l'erreur réelle, il pourrait être utile d'afficher la valeur de ratio, qui se révèle être 0. Le problème est sur la ligne 4, où l'on utilise la division entière au lieu de la division en virgule flottante. Du coup, ratio est nul (au lieu de valoir 0,9), et l'erreur survient parce que la fonction logarithme n'est pas définie pour la valeur 0.

Vous devez prendre le temps de lire attentivement les messages d'erreur, mais ne présumez pas que tout ce qu'ils disent est correct.

• division entière : un opérateur, noté //, qui divise un nombre par un autre et arrondit le résultat vers le bas (vers zéro) à un nombre entier.
• opérateur modulo : un opérateur, noté avec un signe pour cent (%), qui fonctionne sur les nombres entiers et renvoie le reste de la division d'un nombre par un autre.
• expression booléenne : une expression dont la valeur est soit True, soit False.
• opérateur relationnel : un opérateur qui compare ses opérandes, ==, !=, >, <, >= et <=.
• opérateur logique : un opérateur qui combine des expressions booléennes and, or, et not.
• instruction conditionnelle : une instruction qui contrôle le flux d'exécution en fonction de certaines conditions.
• condition : l'expression booléenne dans une instruction conditionnelle, qui détermine quelle branche s'exécute.
• instruction composée : une instruction qui se compose d'une tête et d'un corps. L'en-tête se termine par deux points (:). Le corps est en retrait par rapport à l'en-tête.
• branche : une des séquences successives d'instructions d'une instruction conditionnelle.
• enchaînement de conditions : une instruction conditionnelle avec une série de branches successives.
• instruction conditionnelle imbriquée : une instruction conditionnelle qui apparaît dans l'une des branches d'une autre instruction conditionnelle.
• instruction return : une instruction qui provoque l'arrêt immédiat d'une fonction et le retour à la fonction appelante.
• récursivité : le fait d'appeler la fonction qui est en cours d'exécution.
• cas de base : une branche conditionnelle dans une fonction récursive qui ne fait pas un appel récursif.
• récursion infinie : une récursion qui ne dispose pas d'un cas de base, ou ne l'atteint jamais. En fin de compte, une récursion infinie provoque une erreur d'exécution.

Exercice 1

Le module time fournit une fonction, appelée également time , qui renvoie l'heure GMT par rapport à « l'époque » (epoch), qui est une date arbitraire utilisée comme un point de référence. Sur les systèmes UNIX, epoch est le 1^er janvier 1970. Autrement dit, la fonction time renvoie donc à un instant donné le nombre de secondes écoulées depuis l'époque.

>>> import time
>>> time.time()
1437746094.5735958

Écrivez un script qui lit l'heure actuelle et la convertit en un moment de la journée en heures, minutes et secondes, plus le nombre de jours depuis l'époque.

Exercice 2

Le dernier théorème de Fermat dit qu'il n'existe pas de nombres entiers positifs a, b, et c tels que

pour toute valeur de n supérieure à 2.

1. Écrivez une fonction nommée verifie_fermat qui prend quatre paramètres - a , b , c et n - et vérifie si le théorème de Fermat se vérifie pour ces valeurs. Si n est supérieur à 2 et kitxmlcodeinlinelatexdvpa^{n} + b^{n} = c^{n}finkitxmlcodeinlinelatexdvp le programme doit afficher, « Bon sang, Fermat avait tort ! ». Sinon, le programme doit afficher « Non, cela ne marche pas. »
2. Écrivez une fonction qui invite l'utilisateur à saisir les valeurs de a , b , c et n , les convertit en nombres entiers, et utilise verifie_fermat pour vérifier si elles enfreignent le théorème de Fermat.

Exercice 3

Si l'on vous donne trois bâtons, vous pouvez être en mesure de les organiser dans un triangle, ou pas. Par exemple, si l'un des bâtons a une longueur de 12 centimètres et les deux autres ont un centimètre de long, vous ne serez pas en mesure de faire en sorte que les bâtons courts se rencontrent au milieu. Pour trois longueurs quelconques, il existe un test simple pour savoir s'il est possible de former un triangle :

Si l'une des trois longueurs est supérieure à la somme des deux autres, alors vous ne pouvez pas former un triangle. Sinon, vous pouvez. (Si la somme des deux longueurs est égale à la troisième, elles forment ce qu'on appelle un triangle « aplati » ou « dégénéré ».)

1. Écrivez une fonction nommée is_triangle qui prend comme arguments trois entiers, et qui imprime « Oui » ou « Non », selon que vous pouvez ou ne pouvez pas former un triangle avec des bâtons ayant les longueurs données.
2. Écrivez une fonction qui demande à l'utilisateur de saisir trois longueurs, les convertit en nombres entiers, et utilise is_triangle pour vérifier si les bâtons de longueurs données peuvent former un triangle.

Exercice 4

Quelle est la sortie du programme suivant ? Dessinez un diagramme de pile qui montre l'état du programme lorsqu'il affiche le résultat.

def recurse(n, s):
    if n == 0:
        print(s)
    else:
        recurse(n-1, n+s)

recurse(3, 0)

1. Qu'arriverait-il si vous avez appelé cette fonction comme ceci : recurse(-1, 0)  ?
2. Écrivez une docstring qui explique tout ce que quelqu'un devrait savoir pour utiliser cette fonction (et rien d'autre).

Les exercices suivants utilisent le module turtle, décrit dans le chapitre 4Étude de cas : conception d'une interface :

Exercice 5

Lisez la fonction suivante et voyez si vous pouvez comprendre ce qu'elle fait. Puis exécutez-la (voir les exemples dans le chapitre  4Étude de cas : conception d'une interface ).

def dessiner(t, longueur, n):
    if n == 0:
        return
    angle = 50
    t.fd(longueur * n)
    t.lt(angle)
    dessiner(t, longueur, n-1)
    t.rt(2 * angle)
    dessiner(t, longueur, n-1)
    t.lt(angle)
    t.bk(longueur * n)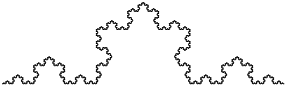

Exercice 6

La courbe de Koch est une fractale qui ressemble à la figure 5.2. Pour dessiner une courbe de Koch de longueur x, tout ce que vous avez à faire est de

1. Dessiner une courbe de Koch avec une longueur x / 3.
2. Tourner à gauche 60 degrés.
3. Dessiner une courbe de Koch avec une longueur x / 3.
4. Tourner à droite 120 degrés.
5. Dessiner une courbe de Koch avec une longueur x / 3.
6. Tourner à gauche 60 degrés.
7. Dessiner une courbe de Koch avec une longueur x / 3.

L'exception est si x est inférieur à 3 : dans ce cas, vous pouvez uniquement tracer une ligne droite d'une longueur x.

1. Écrivez une fonction appelée koch qui prend comme paramètres une tortue et une longueur, et qui utilise la tortue pour dessiner une courbe de Koch avec la longueur donnée.
2. Écrivez une fonction appelée snowflake qui dessine trois courbes de Koch pour faire l'ébauche d'un flocon de neige.
   Solution : koch.py.
3. La courbe de Koch peut être généralisée à plusieurs égards. Voir https://fr.wikipedia.org/wiki/Flocon_de_Koch (voir aussi https://en.wikipedia.org/wiki/Koch_snowflake ) pour des exemples et mettez en œuvre votre favori.