Pensez en Python

Pour vérifier si vous disposez du module turtle, ouvrez l'interpréteur Python et tapez

>>> import turtle
>>> bob = turtle.Turtle()

Créez un fichier nommé monpolygone.py et tapez-y le code suivant :

import turtle
bob = turtle.Turtle()
print(bob)
turtle.mainloop()

Le module turtle (avec un « t » minuscule) fournit une fonction appelée Turtle (avec un « T » majuscule), qui crée un objet Turtle, que nous affectons à une variable nommée bob. L'affichage de bob donnera quelque chose comme :

<turtle.Turtle object at 0xb7bfbf4c>

Cela signifie que bob stocke la référence d'un objet de type Turtle, défini dans le module turtle.

mainloop demande à la fenêtre d'attendre que l'utilisateur fasse quelque chose, bien que, dans ce cas, l'utilisateur n'ait pas grand-chose à faire, sinon fermer la fenêtre.

Une fois que vous créez un objet Turtle, vous pouvez appeler une méthode pour le déplacer autour de la fenêtre. Une méthode ressemble à une fonction, mais utilise une syntaxe légèrement différente. Par exemple, pour faire avancer la tortue :

bob.fd(100)

La méthode fd (forward) est associée à l'objet Turtle que nous nommons bob. Appeler une méthode, c'est comme faire une demande : vous demandez à bob d'avancer.

L'argument de fd est une distance en pixels, sa taille réelle dépend donc de votre écran.

Vous pouvez appeler d'autres méthodes sur un objet Tortue comme : bk (backward) pour reculer, lt (left turn) pour tourner à gauche, et rt (right turn) pour tourner à droite. L'argument des méthodes lt et rt est un angle en degrés.

En outre, chaque Tortue a un « stylo », qui est descendu ou relevé ; si le stylo est descendu, la Tortue laisse une trace lorsqu'elle se déplace. Les méthodes pu et pd correspondent à « pen up » (stylo levé) et « pen down » (stylo descendu).

Pour dessiner un angle droit, ajoutez ces lignes au programme (après la création de bob et avant d'appeler mainloop) :

bob.fd(100)
bob.lt(90)
bob.fd(100)

Lorsque vous exécutez ce programme, vous devriez voir bob aller vers l'est (la droite), puis vers le nord, laissant derrière deux segments de ligne.

Maintenant, modifiez le programme pour dessiner un carré. Ne poursuivez pas avant d'avoir réussi à le faire !

Vous avez probablement écrit quelque chose comme ceci :

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)
bob.lt(90)

bob.fd(100)

Nous pouvons faire la même chose de manière plus concise en utilisant une instruction for. Ajoutez cet exemple à monpolygone.py et exécutez-le à nouveau :

for i in range(4):
    print('Hello!')

Vous devriez voir quelque chose comme ceci :

Hello!
Hello!
Hello!
Hello!

C'est l'utilisation la plus simple de l'instruction for ; nous en verrons plus à ce sujet plus tard. Mais cela devrait suffire pour vous permettre de réécrire votre programme de dessin d'un carré. Ne poursuivez pas avant d'avoir réussi à le faire !

Voici une instruction for qui dessine un carré :

for i in range(4):
    bob.fd(100)
    bob.lt(90)

La syntaxe d'une instruction for ressemble à une définition de fonction. Elle a un en-tête qui se termine par un deux-points et un corps indenté. Le corps peut contenir un nombre quelconque d'instructions.

Une instruction for est également appelée une boucle, parce que le flux d'exécution traverse le corps, puis reboucle vers le haut. Dans notre cas, le corps de la boucle est exécuté à quatre reprises.

Cette version du code du dessin du carré est en fait un peu différente de la précédente, car il y a un dernier virage à gauche après avoir dessiné le dernier côté du carré. Ce virage supplémentaire prend plus de temps, mais faire à chaque fois la même chose dans la boucle simplifie le code. Un autre effet de cette version est de laisser la tortue dans la position de départ, orientée dans la direction de départ.

Ce qui suit est une série d'exercices utilisant TurtleWorld. Ils sont censés être amusants, mais ils ont aussi une raison. Pendant que vous les effectuez, réfléchissez à leur raison.

Les solutions aux exercices se trouvent dans les sections suivantes, alors ne poursuivez pas avant d'avoir fini (ou au moins essayé).

1. Écrivez une fonction appelée carre qui prend un paramètre nommé t, qui est une tortue. Elle doit utiliser la tortue pour dessiner un carré.
   Écrivez un appel de fonction qui passe bob comme argument à carre, puis exécutez à nouveau le programme.
2. Ajoutez à carre un deuxième paramètre, nommé longueur. Modifiez le corps de la fonction afin que la longueur des côtés soit longueur, puis modifiez l'appel de la fonction pour fournir un deuxième argument. Exécutez à nouveau le programme. Testez votre programme avec une plage de valeurs pour longueur.
3. Faites une copie de carre et changez son nom en polygone. Ajoutez-lui un autre paramètre, nommé n, et modifiez-en le corps de sorte qu'il dessine un polygone régulier à n côtés. Indice : Les angles extérieurs d'un polygone régulier à n côtés ont 360/n degrés.
4. Écrivez une fonction appelée cercle, qui prend comme paramètres une tortue t, et le rayon r, et qui dessine un cercle approximatif en appelant polygone avec une longueur et un nombre de côtés approprié. Testez votre fonction avec une gamme de valeurs de r.
   Indice : calculez la circonférence du cercle et assurez-vous que longueur * n = circonference.
5. Faites une version plus générale de cercle, appelée arc, qui prend un paramètre supplémentaire angle, qui détermine quelle fraction d'un cercle dessiner. angle est mesuré en degrés, donc lorsque angle = 360, arc doit dessiner un cercle complet.

Le premier exercice vous demande de mettre votre code qui dessine un carré dans une définition de fonction et ensuite appeler la fonction, en passant la tortue comme paramètre. Voici une solution :

def carre(t):
    for i in range(4):
        t.fd(100)
        t.lt(90)

carre(bob)

Les instructions les plus intérieures, fd et lt, sont indentées deux fois pour montrer qu'elles sont à l'intérieur de la boucle for, qui se trouve à l'intérieur de la définition de fonction. La ligne suivante, carre(bob), est alignée sur la marge gauche, ce qui indique à la fois la fin de la boucle et de la définition de fonction.

À l'intérieur de la fonction, t est la référence de la même tortue bob, de sorte que t.lt(90) a le même effet que bob.lt(90). Dans ce cas, pourquoi ne pas appeler ce paramètre bob ? L'idée est que t peut être n'importe quelle tortue, pas seulement bob, donc vous pouvez créer une deuxième tortue et la passer comme argument à carre :

alice = Turtle()
carre(alice)

Envelopper un morceau de code dans une fonction s'appelle l'encapsulation. L'un des avantages de l'encapsulation est qu'elle attache un nom au code, qui sert comme une sorte de documentation. Un autre avantage est que si vous réutilisez le code, il est plus concis d'appeler une fonction deux fois que de copier et coller le corps !

L'étape suivante consiste à ajouter un paramètre longueur à carre. Voici une solution :

def carre(t, longueur):
    for i in range(4):
        t.fd(longueur)
        t.lt(90)

carre(bob, 100)

L'ajout d'un paramètre à une fonction s'appelle une généralisation, car il rend la fonction plus générale : dans la version précédente, le carré a toujours la même taille ; dans cette nouvelle version, il peut avoir n'importe quelle taille.

L'étape suivante est également une généralisation. Au lieu de dessiner des carrés, polygone dessine des polygones réguliers ayant un nombre quelconque de côtés. Voici une solution :

def polygone(t, n, longueur):
    angle = 360 / n
    for i in range(n):
        t.fd(longueur)
        t.lt(angle)

polygone(bob, 7, 70)

Cet exemple dessine un polygone à sept côtés, avec une longueur de côté de 70.

Si vous utilisez Python 2, la valeur de angle peut être incorrecte à cause de la division entière. Une solution simple consiste à calculer angle = 360.0 / n. Comme le numérateur est un nombre à virgule flottante, le résultat est en virgule flottante.

Lorsqu'une fonction a plus que quelques arguments numériques, il est facile d'oublier ce qu'ils sont, ou l'ordre dans lequel ils devraient être. Dans ce cas, c'est souvent une bonne idée d'inclure les noms des paramètres dans la liste d'arguments :

polygone(bob, n=7, longueur=70)

Ceux-ci sont appelés arguments nommés ou arguments mot-clé, car ils incluent les noms de paramètres comme « mots-clés » (à ne pas les confondre avec les mots-clés Python comme while et def).

Cette syntaxe rend le programme plus lisible. Elle représente aussi un rappel de la façon dont les arguments et les paramètres fonctionnent : lorsque vous appelez une fonction, les arguments sont affectés aux paramètres.

L'étape suivante consiste à écrire cercle, qui prend comme un paramètre un rayon r. Voici une solution simple, qui utilise polygone pour dessiner un polygone à 50 côtés :

import math
				
def cercle(t, r):
    circonference = 2 * math.pi * r
    n = 50
    longueur = circonference / n
    polygone(t, n, longueur)

La première ligne calcule la circonférence d'un cercle de rayon r en utilisant la formule 2 π r. Puisque nous utilisons math.pi, nous devons importer math. Par convention, les instructions import sont généralement au début du script.

n est le nombre de segments de ligne dans notre approximation d'un cercle, donc longueur est la longueur de chaque segment. Ainsi, polygone dessine un polygone à 50 côtés qui sera la représentation approximative d'un cercle de rayon r.

Une limitation de cette solution est que n est une constante, ce qui signifie que pour de très grands cercles, les segments de ligne sont trop longs, et pour les petits cercles, nous gaspillons du temps à dessiner de très petits segments. Une solution serait de généraliser la fonction en prenant comme paramètre n. Cela donnerait à l'utilisateur (celui qui appelle cercle) plus de contrôle, mais l'interface serait moins propre.

L'interface d'une fonction est un résumé de la façon dont elle est utilisée : quels sont les paramètres ? Qu'est-ce que la fonction fait ? Et quelle est la valeur de retour ? Une interface est « propre » si elle permet à l'appelant de faire ce qu'il veut, sans se préoccuper des détails inutiles.

Dans cet exemple, r appartient à l'interface, car il spécifie le rayon du cercle à dessiner. n est moins approprié, car il concerne les détails de la façon dont le cercle doit être dessiné.

Plutôt que d'encombrer l'interface, il est préférable de choisir une valeur appropriée de n en fonction de circonference :

def cercle(t, r):
    circonference = 2 * math.pi * r
    n = int(circonference / 3) + 1
    longueur = circonference / n
    polygone(t, n, longueur)

Maintenant, le nombre de segments est un nombre entier près de circonference / 3, donc la longueur de chaque segment est d'environ 3, assez petite pour que les cercles aient l'air bien circulaires, mais assez grande pour être efficace et acceptable pour des cercles de toutes tailles.

Lorsque je l'ai écrit cercle, je pouvais réutiliser polygone, car un polygone à nombreux côtés est une bonne approximation d'un cercle. Mais arc est plus récalcitrant : nous ne pouvons pas utiliser polygone ou cercle pour dessiner un arc.

Une solution possible est de commencer avec une copie de polygone et la transformer en arc. Le résultat pourrait ressembler à ceci :

def arc(t, r, angle):
    longueur_arc = 2 * math.pi * r * angle / 360
    n = int(longueur_arc / 3) + 1
    longueur_etape = longueur_arc / n
    angle_etape = angle / n
    
    for i in range(n):
        t.fd(longueur_etape)
        t.lt(angle_etape)

La seconde moitié de cette fonction ressemble à polygone, mais nous ne pouvons pas réutiliser polygone sans modifier l'interface. Nous pourrions généraliser polygone pour qu'elle prenne un angle comme troisième argument, mais alors polygone ne serait plus un nom approprié ! Au lieu de cela, nous allons appeler cette fonction plus générale polyligne :

def polyligne(t, n, longueur, angle):
    for i in range(n):
        t.fd(longueur)
        t.lt(angle)

Maintenant, nous pouvons réécrire polygone et arc pour utiliser polyligne :

def polygone(t, n, longueur):
    angle = 360.0 / n
    polyligne(t, n, longueur, angle)

def arc(t, r, angle):
    longueur_arc = 2 * math.pi * r * angle / 360
    n = int(longueur_arc / 3) + 1
    longueur_etape = longueur_arc / n
    angle_etape = float(angle) / n
    polyligne(t, n, longueur_etape, angle_etape)

Enfin, nous pouvons réécrire cercle pour utiliser arc :

def cercle(t, r):
    arc(t, r, 360)

Ce processus - le réarrangement d'un programme visant à améliorer les interfaces et à faciliter la réutilisation du code - est appelé réusinage (ou parfois refactorisation). Dans ce cas, nous avons remarqué qu'il y avait un code similaire tant en arc qu'en polygone, alors nous l'avons déplacé dans polyligne.

Si nous avions planifié dès le début, nous aurions peut-être écrit d'abord polyligne et évité le réusinage, mais souvent vous n'en savez pas assez au début d'un projet pour concevoir toutes les interfaces. Une fois que vous commencez à coder, vous comprenez mieux le problème. Parfois, le réusinage est un signe que vous avez appris quelque chose.

Un plan de développement est un processus pour écrire des programmes. Le processus que nous avons utilisé dans cette étude de cas est « l'encapsulation et la généralisation ». Les étapes de ce processus sont :

1. Commencer par écrire un petit programme sans aucune définition de fonction ;
2. Une fois que votre programme fonctionne, identifier un composant cohérent, l'encapsuler dans une fonction et lui donner un nom ;
3. Généraliser la fonction en ajoutant des paramètres appropriés ;
4. Répéter les étapes 1-3 jusqu'au moment où vous avez un ensemble de fonctions qui font ce que vous souhaitez. Copier et coller le code fonctionnel pour éviter de retaper (et de déboguer à nouveau) ;
5. Chercher des opportunités d'améliorer le programme par réusinage. Par exemple, si vous avez un code similaire à plusieurs endroits, envisagez de le factoriser dans une fonction générale appropriée.

Ce processus a quelques inconvénients - nous allons voir d'autres options plus tard -, mais il peut être utile si vous ne savez pas à l'avance comment diviser le programme en fonctions. Cette approche vous permet de concevoir pendant que vous avancez.

Une docstring est un texte au début d'une fonction qui explique l'interface (« doc » est l'abréviation de « documentation »). Voici un exemple :

def polyligne(t, n, longueur, angle):
    """Dessine n segments de ligne ayant la longueur et l'angle 
    entre eux (en degrés) donnés. t est une tortue.
    """    
    for i in range(n):
        t.fd(longueur)
        t.lt(angle)

Par convention, toutes les docstrings sont des chaînes entourées par des guillemets triples, également connues comme des chaînes multilignes, parce que les guillemets triples permettent l'écriture de la chaîne sur plusieurs lignes.

La docstring ci-dessus est laconique, mais contient les informations essentielles dont quelqu'un aurait besoin pour utiliser cette fonction. Elle explique de façon concise ce que fait la fonction (sans entrer dans les détails de comment elle le fait). Elle explique l'effet de chaque paramètre sur le comportement de la fonction et de quel type doit être chaque paramètre (si cela n'est pas évident).

La rédaction de ce type de documentation est une partie importante de la conception de l'interface. Une interface bien conçue doit être simple à expliquer ; si vous avez du mal à expliquer l'une de vos fonctions, peut-être l'interface devrait-elle être améliorée.

Une interface est comme un contrat entre une fonction et un appelant. L'appelant accepte de fournir certains paramètres et la fonction accepte de faire un certain travail.

Par exemple, polyligne nécessite quatre arguments : t doit être une tortue, n doit être un nombre entier, longueur doit être un nombre positif et angle doit être un nombre qui peut être compris comme étant en degrés.

Ces exigences sont appelées préconditions, parce qu'elles sont censées être vraies avant que la fonction commence à être exécutée. Inversement, les conditions à la fin de la fonction sont des postconditions. Les postconditions incluent l'effet escompté de la fonction (comme le dessin des segments de ligne) et des effets secondaires (comme déplacer la tortue ou d'autres changements).

Les préconditions ou conditions préalables sont à la charge de l'appelant. Si l'appelant viole une précondition (correctement documentée !) et la fonction ne marche pas correctement, le bogue est dans l'appelant, et pas dans la fonction.

Si les préconditions sont satisfaites et les postconditions ne le sont pas, le bogue est dans la fonction. Si vos préconditions et vos postconditions sont claires, elles peuvent aider au débogage.

• méthode : une fonction qui est associée à un objet et appelée en utilisant la notation pointée.
• boucle : une partie d'un programme qui peut être exécutée à plusieurs reprises.
• encapsulation : le processus de transformation d'une séquence d'instructions en une définition de fonction.
• généralisation : le processus qui consiste à remplacer quelque chose d'inutilement spécifique (comme un nombre) par quelque chose de convenablement général (comme une variable ou un paramètre).
• argument mot-clé : un argument qui inclut le nom du paramètre comme un « mot-clé ».
• interface : une description de la façon d'utiliser une fonction, y compris les noms et les descriptions des arguments et la valeur de retour.
• réusinage : le processus de modification d'un programme qui fonctionne pour améliorer les interfaces des fonctions et d'autres qualités du code.
• plan de développement : un procédé pour l'écriture de programmes.
• docstring : une chaîne qui apparaît au début d'une définition de fonction afin de documenter l'interface de la fonction.
• précondition (condition préalable) : une exigence qui doit être satisfaite par l'appelant avant l'exécution d'une fonction.
• postcondition : une exigence qui doit être satisfaite par la fonction avant sa fin.

Exercice 1

Téléchargez le code de ce chapitre à partir de polygon.py.

1. Dessinez un diagramme de pile qui montre l'état du programme lors de l'exécution de circle(bob, radius) . Vous pouvez faire le calcul à la main ou ajouter des instructions print au code.
2. La version de arc dans la Section  4.7.Réusinage n'est pas très précise parce que l'approximation linéaire du cercle est toujours en dehors du vrai cercle. En conséquence, la tortue s'arrête à une distance de quelques pixels de la destination correcte. Ma solution montre un moyen de réduire l'effet de cette erreur. Lisez le code et voyez si cela a du sens pour vous. Si vous dessinez un diagramme, cela pourra vous aider à voir comment cela fonctionne.

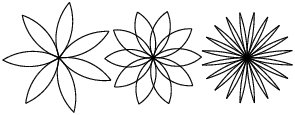
Exercice 2

Écrivez un ensemble convenablement général de fonctions qui peuvent dessiner des fleurs comme dans la Figure 4.1.

Solution: flower.py, exige également polygon.py.

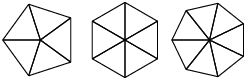
Exercice 3

Écrivez un ensemble convenablement général de fonctions qui peuvent dessiner des formes comme dans la Figure 4.2.

Exercice 4

Les lettres de l'alphabet peuvent être construites à partir d'un nombre modéré d'éléments de base, comme les lignes verticales et horizontales et quelques courbes. Concevez un alphabet qui peut être dessiné avec un nombre minimal d'éléments de base et ensuite écrivez les fonctions qui dessinent les lettres.

Vous devriez écrire une fonction pour chaque lettre, ayant les noms dessiner_a , dessiner_b , etc., et mettre vos fonctions dans un fichier nommé letters.py . Vous pouvez télécharger une « tortue - machine à écrire » à typewriter.py pour vous aider à tester votre code.

Vous pouvez obtenir une solution à l'adresse letters.py ; elle exige aussi polygon.py.

Exercice 5

Lisez à propos de spirales à l'adresse https://fr.wikipedia.org/wiki/Spirale (voir aussi http://en.wikipedia.org/wiki/Spiral) ; ensuite, écrivez un programme qui dessine une spirale d'Archimède (ou l'un des autres types de spirales). Solution: spiral.py.