Pensez en Python

Comme vous avez pu le découvrir, il est permis d'assigner plus d'une valeur à la même variable. Une nouvelle affectation permet à une variable existante de faire référence à une nouvelle valeur (et de cesser de faire référence à l'ancienne valeur).

>>> x = 5
>>> x
5
>>> x = 7
>>> x
7

Lorsque nous affichons x la première fois, sa valeur est 5 ; la seconde fois, sa valeur est 7.

La figure 7.1 montre à quoi ressemble une réaffectation dans un diagramme d'état.

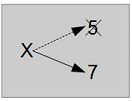
À ce stade, je voudrais aborder une source de confusion commune. Comme Python utilise le signe égal (=) pour l'affectation, il est tentant d'interpréter une instruction du genre a = b comme une proposition mathématique d'égalité ; à savoir l'affirmation selon laquelle a et b sont égaux. Mais cette interprétation est erronée.

Premièrement, l'égalité est une relation symétrique et l'affectation ne l'est pas. Par exemple, en mathématiques si a = 7, alors 7 = a. Mais en Python, l'instruction a = 7 est autorisée et 7 = a ne l'est pas.

En plus, en mathématiques une proposition d'égalité est toujours soit vraie, soit fausse. Si a = b maintenant, alors a sera toujours égal à b. En Python, une instruction d'affectation peut rendre égales deux variables, mais rien ne les oblige à rester égales :

>>> a = 5
>>> b = a    # a et b sont égales maintenant
>>> a = 3    # a et b ne sont plus égales
>>> b
5

La troisième ligne modifie la valeur de a, mais ne modifie pas la valeur de b, et les deux variables ne sont donc plus égales.

La réaffectation des variables est souvent utile, mais vous devez l'utiliser avec prudence. Si la valeur des variables change fréquemment, cela peut rendre le code difficile à lire et à déboguer.

Un genre commun de réaffectation est une mise à jour, où la nouvelle valeur de la variable dépend de l'ancienne.

>>> x = x + 1

Cela signifie « prenez la valeur actuelle de x, ajoutez-y 1, puis mettez à jour x avec la nouvelle valeur ».

Si vous essayez de mettre à jour une variable qui n'existe pas, vous obtenez une erreur, parce que Python évalue le côté droit avant d'attribuer une valeur à x :

>>> x = x + 1
NameError: name 'x' is not defined

Avant de pouvoir mettre à jour une variable, vous devez l'initialiser, habituellement avec une instruction simple :

>>> x = 0
>>> x = x + 1

La mise à jour d'une variable en ajoutant 1 à sa valeur s'appelle une incrémentation ; la soustraction de 1 est appelée décrémentation.

Les ordinateurs sont souvent utilisés pour automatiser des tâches répétitives. Répéter des tâches identiques ou similaires sans faire d'erreur est quelque chose que les ordinateurs font bien et que les gens font mal. Dans un programme d'ordinateur, la répétition s'appelle aussi itération.

Nous avons vu déjà deux fonctions, compte_a_rebours et print_n, qui itèrent en utilisant la récursivité. Comme l'itération est une tâche très commune, Python fournit des fonctionnalités de langage pour la rendre plus facile. L'une d'entre elles est l'instruction for, que nous avons vue dans la section 4.2Répétition simple. Nous y reviendrons plus tard.

Une autre est l'instruction while (tant que). Voici une version du compte_a_rebours qui utilise une instruction while :

def compte_a_rebours(n):
    while n > 0:
        print(n)
        n = n - 1
    print('Décollez !')

Vous pouvez presque lire l'instruction while comme si c'était une phrase écrite en anglais. Cela signifie « Tant que n est supérieur à 0, affichez la valeur de n, puis décrémentez n. Lorsque vous arrivez à 0, affichez le mot Décollez ! ».

Plus formellement, voici le flux d'exécution pour une instruction while :

1. Déterminer si la condition est vraie ou fausse ;
2. Si elle est fausse, sortir de l'instruction while et poursuivre l'exécution à l'instruction suivante ;
3. Si la condition est vraie, exécutez le corps, puis retournez à l'étape 1.

Ce type de flux s'appelle une boucle parce que la troisième étape reboucle vers le haut.

Le corps de la boucle doit modifier la valeur d'une ou plusieurs variables de sorte que la condition devienne finalement fausse et que la boucle se termine. Sinon, la boucle se répète pour toujours et s'appelle une boucle infinie. Une source inépuisable de divertissement pour les informaticiens est l'observation que les instructions sur le shampooing, « Faire mousser, rincer, répéter », sont une boucle infinie.

Dans le cas de compte_a_rebours, nous pouvons prouver que la boucle se termine : si n est zéro ou négatif, la boucle n'est jamais exécutée. Sinon, n devient plus petit à chaque itération de la boucle, donc, finalement, nous devons arriver à 0.

Pour certaines autres boucles, ce n'est pas si facile à dire. Par exemple :

def sequence(n):
    while n != 1:
        print(n)
        if n % 2 == 0:        # n est pair
            n = n / 2
        else:                 # n est impair
            n = n * 3 + 1

La condition de cette boucle est n != 1, donc la boucle continuera jusqu'à ce que n soit 1, ce qui rend la condition fausse.

À chaque passage dans la boucle, le programme affiche la valeur de la variable n, puis vérifie si celle-ci est paire ou impaire. Si n est pair, il est divisé par 2. Si n est impair, sa valeur est remplacée par n * 3 + 1. Par exemple, si l'argument passé à sequence est 3, les valeurs de n résultantes sont 3, 10, 5, 16, 8, 4, 2, 1.

Puisque n tantôt augmente, tantôt diminue, il n'y a aucune preuve évidente qu'un jour n sera 1, ou que le programme se terminera. Pour certaines valeurs particulières de n, nous pouvons prouver la fin du programme. Par exemple, si la valeur de départ est une puissance de deux, n sera pair à chaque passage dans la boucle jusqu'à ce qu'il atteigne 1. L'exemple précédent se termine par une telle séquence, en commençant par 16.

La question difficile est de savoir si nous pouvons prouver que ce programme se termine pour toutes les valeurs positives de n. Jusqu'à présent, personne n'a été en mesure de le prouver ou de le réfuter ! (Voir https://fr.wikipedia.org/wiki/Conjecture_de_Syracuse.)

À titre d'exercice, réécrivez la fonction afficher_n de la section 5.8Récursion en utilisant l'itération au lieu de la récursivité.

Parfois, vous ne savez pas qu'il est temps de mettre fin à une boucle avant d'arriver à mi-chemin du corps de la boucle au cours d'une itération donnée. Dans ce cas, vous pouvez utiliser l'instruction break pour sortir de la boucle.

Par exemple, supposons que vous vouliez prendre une saisie au clavier d'un utilisateur jusqu'à ce qu'il tape fini. Vous pourriez écrire :

while True:
    ligne = input('> ')
    if ligne == 'fini':
        break
    print(ligne)

print('Fini !')

La condition de la boucle est True, qui est toujours vraie, donc la boucle s'exécute jusqu'à ce qu'elle atteigne l'instruction break.

À chaque itération, elle affiche à l'utilisateur l'invite >. Si l'utilisateur tape fini, l'instruction break provoque la sortie de la boucle. Sinon, le programme affiche à l'écran tout ce qu'écrit l'utilisateur et remonte au début de la boucle. Voici un exemple d'exécution :

> pas fini
pas fini
> fini
Fini !

Cette façon d'écrire des boucles while est commune parce que vous pouvez vérifier la condition n'importe où dans la boucle (et pas seulement en début) et vous pouvez exprimer la condition d'arrêt affirmativement (« arrêter quand cela arrive ») plutôt que négativement (« continuer jusqu'à ce que cela se passe »).

Les boucles sont souvent utilisées dans des programmes qui calculent des résultats numériques en commençant avec une réponse approximative et l'améliorant de manière itérative.

Par exemple, une façon de calculer des racines carrées est la méthode de Newton. Supposons que vous vouliez trouver la racine carrée de a. Si vous commencez avec une estimation quelconque, x, vous pouvez calculer une meilleure estimation en utilisant la formule suivante :

Par exemple, si a est 4 et x est 3 :

>>> a = 4
>>> x = 3
>>> y = (x + a/x) / 2
>>> y
2.16666666667

Le résultat est plus proche de la bonne réponse (√4 = 2). Si nous répétons le processus avec la nouvelle estimation, le résultat se rapproche encore plus :

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00641025641

Après encore quelques itérations, l'estimation est presque exacte :

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00001024003
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00000000003

En général, nous ne savons pas à l'avance combien d'étapes il faudra pour arriver à la bonne réponse, mais nous savons quand nous y arrivons, car l'estimation cesse de changer :

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0

Lorsque y == x, nous pouvons arrêter. Voici une boucle qui commence par une première estimation, x, et améliore celle-ci jusqu'à ce qu'elle arrête de changer :

while True:
    print(x)
    y = (x + a/x) / 2
    if y == x:
        break
    x = y

Pour la plupart des valeurs de a, ceci fonctionne très bien, mais en général, il est dangereux de tester l'égalité des float. Les valeurs à virgule flottante ne sont qu'approximativement exactes : la majorité des nombres rationnels, comme 1/3, et irrationnels, comme √2, ne peuvent pas être représentés exactement avec un float.

Plutôt que de vérifier si x et y sont exactement égaux, il est plus sûr d'utiliser la fonction interne abs pour calculer la valeur absolue, ou l'ampleur, de la différence entre eux :

    if abs(y-x) < epsilon:
        break

Où epsilon a une valeur comme 0,0000001 qui détermine à partir de quand on estime être suffisamment proche de l'égalité.

La méthode de Newton est un exemple d'un algorithme : un processus mécanique pour résoudre une catégorie de problèmes (dans ce cas, le calcul des racines carrées).

Pour comprendre que c'est un algorithme, cela pourrait aider de commencer par quelque chose qui n'est pas un algorithme. Lorsque vous avez appris à multiplier les nombres à un chiffre, vous avez probablement mémorisé la table de multiplication. En effet, vous avez mémorisé 100 solutions spécifiques. Ce genre de connaissances n'est pas de l'algorithmique.

Mais si vous étiez « paresseux », vous pourriez avoir appris quelques trucs. Par exemple, pour trouver le produit de n et 9, vous pouvez écrire n - 1 comme premier chiffre et 10 - n comme deuxième chiffre. Cette astuce est une solution générale pour multiplier un nombre à un chiffre par 9. C'est un algorithme !

De même, les techniques que vous avez apprises pour l'addition, la soustraction ou la division avec retenue sont toutes des algorithmes. L'une des caractéristiques des algorithmes est qu'ils ne nécessitent aucune intelligence particulière pour les effectuer. Ce sont des mécanismes dans lesquels chaque étape découle de la précédente selon un ensemble de règles simples.

L'exécution des algorithmes est ennuyeuse, mais leur conception est intéressante, intellectuellement stimulante, et représente une partie centrale de la science informatique.

Certaines des choses que les gens font naturellement, sans aucune difficulté ou pensée consciente, sont les plus difficiles à exprimer en algorithmique. Comprendre le langage naturel humain est un bon exemple. Nous le faisons tous, mais jusqu'à présent, personne n'a été en mesure d'expliquer comment nous le faisons ni de le formaliser sous la forme d'un algorithme.

Comme vous commencez à écrire des programmes plus volumineux, il se peut que vous arriviez à passer plus de temps à déboguer. Plus de code signifie plus de chances de faire une erreur et plus d'endroits où les bogues peuvent se cacher.

Une façon de réduire votre temps de débogage est le « débogage par dichotomie ». Par exemple, s'il y a 100 lignes de code dans votre programme et vous les vérifiez une par une, il faudra 100 étapes.

Au lieu de cela, essayez de diviser le problème en deux. Recherchez au milieu du programme, ou aux alentours, une valeur intermédiaire que vous pouvez vérifier. Ajoutez une instruction d'affichage (ou autre chose dont l'effet est vérifiable) et exécutez le programme.

Si le résultat de la vérification à mi-chemin est incorrect, il doit y avoir un problème dans la première moitié du programme. S'il est correct, le problème est dans la seconde moitié.

Chaque fois que vous effectuez une vérification de ce genre, vous réduisez de moitié le nombre de lignes que vous devez examiner. Après six étapes (ce qui est nettement moins de 100), vous arriverez à une ou deux lignes de code, du moins en théorie.

En pratique, trouver le « milieu du programme » n'est pas toujours simple et il n'est pas toujours possible de le vérifier. Compter les lignes et trouver le point médian exact n'a pas de sens. Au lieu de cela, pensez à des endroits dans le programme où il pourrait y avoir des erreurs et des endroits où il est facile de faire une vérification. Ensuite, choisissez un endroit où vous pensez qu'il y a des chances approximativement égales que le bogue soit avant ou après la vérification.

• réaffectation : assignation d'une nouvelle valeur à une variable qui existe déjà.
• mise à jour : une affectation où la nouvelle valeur d'une variable dépend de l'ancienne.
• initialisation : une assignation qui donne une valeur initiale à une variable qui sera mise à jour.
• incrémentation : une mise à jour qui augmente la valeur d'une variable (souvent par pas de 1).
• décrémentation : une mise à jour qui diminue la valeur d'une variable.
• itération : exécution répétée d'une série d'instructions en utilisant soit un appel de fonction récursive, soit une boucle.
• boucle infinie : une boucle dans laquelle la condition d'arrêt n'est jamais satisfaite.
• algorithme : un processus général pour résoudre une catégorie de problèmes.

Exercice 1

Copiez la boucle de la section 7.5Racines carrées et encapsulez-la dans une fonction appelée mysqrt qui prend a comme paramètre, choisit une valeur raisonnable de x , et renvoie une estimation de la racine carrée de a .

Pour la tester, écrivez une fonction nommée test_racine_carree qui imprime un tableau comme celui-ci :

a   mysqrt(a)     math.sqrt(a)  diff
-   ---------     ------------  ----
1.0 1.0           1.0           0.0
2.0 1.41421356237 1.41421356237 2.22044604925e-16
3.0 1.73205080757 1.73205080757 0.0
4.0 2.0           2.0           0.0
5.0 2.2360679775  2.2360679775  0.0
6.0 2.44948974278 2.44948974278 0.0
7.0 2.64575131106 2.64575131106 0.0
8.0 2.82842712475 2.82842712475 4.4408920985e-16
9.0 3.0           3.0           0.0

Sur la première colonne se trouve un nombre, a ; la deuxième colonne est la racine carrée de a calculée avec mysqrt ; la troisième colonne est la racine carrée calculée avec math.sqrt ; la quatrième colonne est la valeur absolue de la différence entre les deux estimations.

Exercice 2

La fonction interne eval prend une chaîne de caractères et l'évalue comme du code Python en utilisant l'interpréteur Python. Par exemple :

>>> eval('1 + 2 * 3')
7
>>> import math
>>> eval('math.sqrt(5)')
2.2360679774997898
>>> eval('type(math.pi)')
<class 'float'>

Écrivez une fonction appelée eval_boucle qui invite l'utilisateur de manière itérative à saisir une chaîne de caractères, prend la saisie résultante, l'évalue en utilisant eval et affiche le résultat.

Cela devrait continuer jusqu'à ce que l'utilisateur entre « fini », puis la valeur de la dernière expression évaluée est retournée.

Exercice 3

Le mathématicien Srinivasa Ramanujan a trouvé une série infinie qui peut être utilisée pour générer une approximation numérique de 1 / π :

Écrivez une fonction appelée estimate_pi qui utilise cette formule pour calculer et retourner une estimation de π. Elle doit utiliser une boucle while pour calculer les termes de la somme jusqu'à ce que le dernier terme calculé de la somme soit plus petit que 1e-15 (qui est la notation Python pour 10^-15). Vous pouvez vérifier le résultat en le comparant à math.pi.

Solution : pi.py.